Chapter 4

     In 1859 A.D. John Taylor of London published, The Great Pyramid: Why was it built? And who built it? Although Taylor had not visited the Great Pyramid himself, for over 30 years he had compiled and compared all published accounts and certified measurements of those who had. He theorized that the perimeter of the Great Pyramid measured 36,524.2 polar inches. A polar inch is the polar diameter of Earth divided by 500,000,000 parts, where one part, or one polar inch, is equivalent to 1.001063285 British inches in length. At the time of his proposed theory not Taylor or anyone else knew the length of a polar inch to this level of accuracy, as this precision of the polar inch measurement only became available in the Astronomical Almanac of 2007-2010. If Taylor’s theory were correct, then application of this modern polar inch would mean that the Great Pyramid’s base should measure 36,563.07127 British inches in length, and it has been proposed that a measurement between the outer corners or socket stones of the Great Pyramid would yield this length. Petrie gave these four side distances between socket stones, as N. 9129.8”, E. 9130.8”, S. 9123.9”, and W. 9119.2” for a total 36,503.7 British inches, [4] which distance was 59.37 inches short of Taylor’s theorized distance. Reference the photographs, “Casing Stones North Side of Great Pyramid – View A,” and “View B,” and “Wind Eroded Casing Stones on South Side of Great Pyramid – View A,” and “View B.” Future discussion will demonstrate that Petrie was correct as to the place that he took his measurement, where the casing stones meet the platform, and that Smyth was incorrect as to where he took his measurement, between the outer corners or sockets, as was Taylor in theorizing that the base circuit perimeter of the Great Pyramid was 36,524.2 polar inches.

     The drawing, “Base Perimeter Survey Comparison of Petrie, Cole, and Dorner,” is drawn to scale—actual size. It is within the illustrated five-inch length that the differences compare between the perimeter length measurements from the three surveys of the Great Pyramid. Petrie in 1881 A.D. cleared the four corners, but not the sides of the pyramid. He surveyed the base perimeter measuring 36,275.2 British inches stating an error margin of plus or minus 2.4 inches. The length of the British inch changed on July 1, 1959 A.D., which purpose was to standardize a relationship equivalent to the metric units of measure, and this change would then modify Petrie’s measurement from 36,275.2 to 36,275.23142 British inches. Petrie was followed by Cole who cleared the entire base and measured it in metric units to obtain 921.455 meters, which length is equivalent to 36,277.75591 British inches with a stated error margin of plus or minus 2.44094 British inches. [5] There is a difference of 2.52449 British inches between the center points of the Petrie and Cole surveys. Cole’s is the longer of the two, and as referenced in the drawing their error margins overlap by 2.31645 British inches. The true base length should be within this overlap. It was in 1981 A.D. that Josef Dorner conducted a laser survey of the base perimeter. Egyptologist Mark Lehner refers to the Dorner measurement as “our survey,” and so we understand that he took part in the project. [6] Due to the accuracy obtainable with laser technology Dorner’s measurement should become the reference distance at 921.441 meters, which distance is equivalent to 36,277.20472 British inches. The Dorner survey measurements were N. 230.328 m., E. 230.369 m., S. 230.372 m., and W. 230.372 m. to equal 921.441 meters. [7] The Dorner measurement falls coincidentally, or perhaps expectedly, within the overlap of the Petrie and Cole surveys.

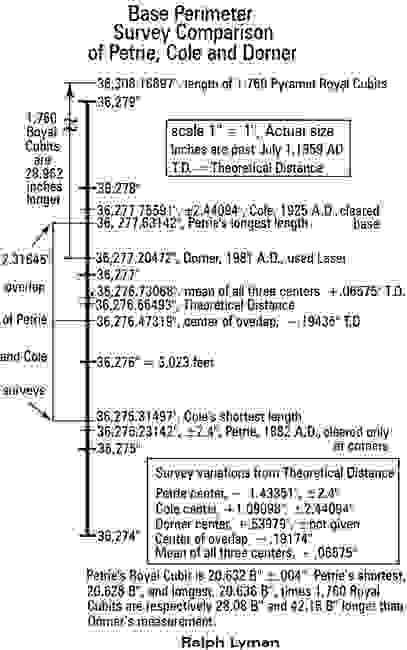
       Using Dorner’s distance, and the royal cubit previously mentioned, let us once again consider the statement of Herodotus; that being, the base length of the Great Pyramid measures 1,760 royal cubits. As heretofore stated the royal cubit is equivalent to 20.62850396 British inches, and when this length is multiplied by the 1,760 royal cubit record of Herodotus it yields a distance of 36,306.16697 British inches. This distance exceeds the Dorner reference distance of 36,277.20472 British inches by 28.96225 British inches. This 28.96225 inch disparity from the Dorner measurement is considerable, so much so that it most likely precludes the Herodotus stated length of 1,760 royal cubits as plausible, and so the Dorner reference distance will hereafter be referred to as the reference distance. 

     There is another theory that is but 0.53979 British inches short of the reference distance. The 0.53979 British inch difference between this theory and the reference distance is only 1/54th the variance of that found in the 1,760 royal cubit theory. As can be seen in the last drawing the base perimeter distance of this unique theory is merely 0.19174 British inches short of the center of the overlap of the Petrie and Cole surveys, and from the mean of all three surveys plus 0.06575 British inches over a 3,023 foot distance. This theory sounds promising.